深度学习_2_梯度下降法

机器学习过程

机器学习算法用于训练模型的迭代试错过程：

假设有时间和计算资源来计算的所有可能的损失值。对于回归问题，所产生的损失和权重值($ w_i $)的关系是凸形的，如下图所示：

凸形问题只有一个最低点：即只存在一个斜率正好为0的位置。这个最小值就是损失函数收敛之处。

通过计算整个数据集中每个可能值的损失函数来找到收敛点这种方法效率太低。机器学习领域有一种找到这个收敛点的机制，叫做梯度下降法。

梯度下降法

梯度下降法的第一个阶段是选择一个起始点值（起点）。起点并不只要，因此很多算法就直接将起点$ w_i $设为0或者随机选择一个值。我们选择一个稍大于0的起点，如下图所示：

然后梯度下降法会计算损失曲线在起点处的梯度。梯度是偏导数的矢量；它可以让我们了解哪个方向距离目标“更近”或者“更远”。需要注意的是，损失相对于单个权重的梯度，就等于导数。

梯度是一个矢量，因此具有如下两个特征：

方向
大小

梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法算法会沿着负梯度的方向走一步，以便尽快降低损失。

为了确定损失函数曲线上的下一个点，梯度下降法算法会将梯度大小的一部分与起点相加，如下图所示：

然后，梯度下降法会重复此过程，逐渐接近最低点。

以上内容整理自：google机器学习速成课程-降低损失 (Reducing Loss)：梯度下降法：https://developers.google.cn/machine-learning/crash-course/reducing-loss/gradient-descent

个人理解

梯度就是为了找一个方向，沿着负梯度方向走梯度乘学习速率（learning rate）(也称步长)的距离，以确定下一个点的位置。

例如，当前点梯度为-2.5，学习速率为0.001,则梯度下降法会选择当前点向右、距离当前点0.025的位置作为下一个点。

如下图所示：

图中A点则往右走一步，即$ w_i $ 加上梯度（正）乘学习速率；图中B点则往左走一步，

计算公式为：$ w_i ＝　w_i －　α　×　dw $。

其中$ α $ 为learning_rate。

梯度的正负决定下一步的计算方向，而梯度的值和学习速率决定下一步的位置

思考

对于上面的图，损失和权重的曲线只有一个最小值，即只有一个点的梯度为0.

但是，也有可能是这种情况：

图中有多个最小值，其中A、B、C、D为局部最小值，G为全局最小值。

如果起始选取的w值为A'或者B'或者C'或者D'，那么损失会在A B C D中的一个收敛，虽然找到了最小值，却不是全局最小值，这样得到的结果肯定不是我们想要的。这样的话，梯度下降法会不会有问题？

解惑

上面损失和w的关系是二维的情况，实际应用中大多是比较复杂的模型，都是多维的，那么多维的场景会不会出现上面的局部最小值呢？比如像下图中所示，会不会出现图中的蓝色点的情况，导致找到的是局部最小值，而不是红色箭头所指的全局最小值？

答案是否定的。

到2014年，一篇论文《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》，指出高维优化问题中根本没有那么多局部极值。作者依据统计物理，随机矩阵理论和神经网络理论的分析，以及一些经验分析提出高维非凸优化问题之所以困难，是因为存在大量的鞍点（梯度为零并且Hessian矩阵特征值有正有负）而不是局部极值。

鞍点（saddle point)如下图（来自http://x-wei.github.io/Ng_DLMooc_c2wk2.html）。

和局部极小值相同的是，在该点处的梯度都等于零，不同在于在鞍点附近Hessian矩阵有正的和负的特征值，即是不定的，而在局部极值附近的Hessian矩阵是正定的。

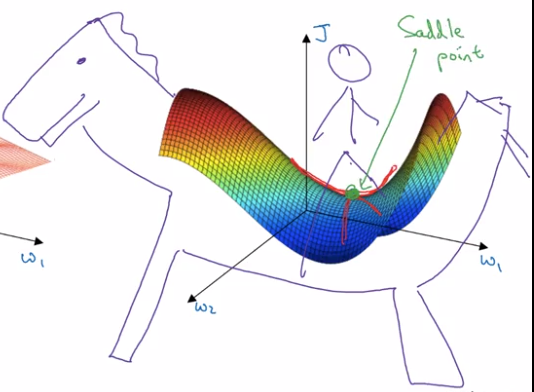
在鞍点附近，基于梯度的优化算法（几乎目前所有的实际使用的优化算法都是基于梯度的）会遇到较为严重的问题，可能会长时间卡在该点附近。在鞍点数目极大的时候，这个问题会变得非常严重（下图来自上面论文）。

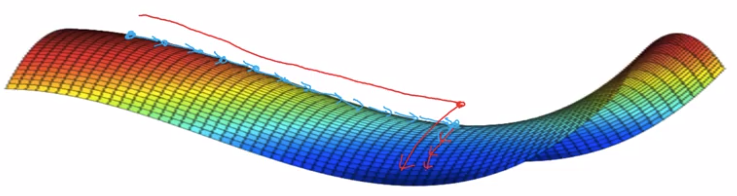
这个问题目前仍有讨论，不过大体上人们接受了这种观点，即造成神经网络难以优化的一个重要（乃至主要）原因是存在大量鞍点。造成局部极值这种误解的原因在于，人们把低维的直观认识直接推到高维的情况。在一维情况下，局部极值是仅有的造成优化困难的情形（Hessian矩阵只有一个特征值）。该如何处理这种情况，目前似乎没有特别有效的方法。

多解释一点

1.鞍点也是驻点，鞍点处的梯度为零，在一定范围内沿梯度下降会沿着鞍点附近走，这个区域很平坦，梯度很小。
2.优化过程不是卡在鞍点不动了(像人们以为的局部极值那样)，而是在鞍点附近梯度很小，于是变动的幅度越来越小，loss看起来就像是卡住了。但是和local minima的差别在于，如果运行时间足够长，SGD一类的算法是可以走出鞍点附近的区域的（看下面的两个链接）。由于这需要很长时间，在loss上看来就像是卡在local minima了。然而，从一个鞍点附近走出来，很可能会很快就进入另一个鞍点附近了。
3.直观来看增加一些扰动，从下降的路径上跳出去就能绕过鞍点。但在高维的情形，这个鞍点附近的平坦区域范围可能非常大。此外，即便从一个鞍点跳过，这个跳出来的部分很可能很快进入另一个鞍点的平坦区域—— 鞍点的数量(可能)是指数级的。各种优化算法在鞍点附近形态的展示，可以看动态图An overview of gradient descent optimization algorithms 最下面的部分，非常生动形象。中文可见SGD，Adagrad，Adadelta，Adam等优化方法总结和比较。

以上内容参考： 1. https://www.zhihu.com/question/52782960/answer/133724696 2. http://x-wei.github.io/Ng_DLMooc_c2wk2.html