Vernlium

Keep codeing and thinking!

0%

leetcode_动态规划题目总结

发表于 更新于

之前对动态规划类型的题目一直很恐惧，拿到题目后没有思路。最近针对动态规划类型的题目做个专项练习，期望拿到这些题目的时候不慌，按照一定的套路分析出解题思路。

动态规划

动态规划题目类型

  • 1.计数
    • 有多少种方式走到右下角
    • 有多少种方式选出k个数使得和是sum
    1. 求最大最小值
    • 从左上角到右下角路径到最大数字和
    • 最长上升子序列长度
    1. 求存在性
    • 取石子游戏，先手是否必胜
    • 能不能选出k个数使得和是sum

动态规划四步骤

  • 确定状态
    • 研究最优策略的最后一步
    • 化为子问题
  • 转移方程
    • 根据子问题定义得到
  • 初始条件和边界情况
  • 计算顺序

常见动态规划类型

  • 坐标型动态规划（20%）
  • 序列型动态规划（20%）
  • 划分型动态规划（20%）
  • 区间型动态规划（15%）
  • 背包型动态规范（10%）
  • 最长序列型动态规划（5%）
  • 博弈型动态规划（5%）
  • 综合型动态规划（5%）

题目实例

Coin Change

跳跃游戏Jump Game

Uniqe Paths

Maximum Product Subarray

实战题目练习

32.最长有效括号

结合题目，有最长这个字眼，可以考虑尝试使用动态规划进行分析。这是一个最值型动态规划的题目。

首先，我们定义一个 \(dp\) 数组，其中第 \(i\) 个元素表示以下标为 \(i\) 的字符结尾的最长有效子字符串的长度。

确定状态

最后一步

对于最优的策略，一定有最后一个元素 \(s[i]\).

所以，我们先看第 \(i\) 个位置，这个位置的元素 \(s[i]\)可能有如下两种情况：

  • \(s[i] == (\) :

    这时，\(s[i]\) 无法和其之前的元素组成有效的括号对，所以，\(dp[i] = 0\)

  • \(s[i] == )\) :

    这时，需要看其前面对元素来判断是否有有效括号对。

    • 情况1:

      \(s[i - 1] == (\)

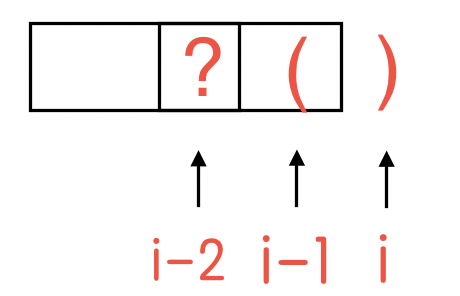
      即 \(s[i]\) 和 \(s[i - 1]\) 组成一对有效括号，有效括号长度新增长度2，\(i\)位置对最长有效括号长度为 其之前2个位置的最长括号长度加上当前位置新增的2，我们无需知道\(i-2\)位置对字符是否可以组成有效括号对。

      那么有：

      \(dp[i] = dp[i - 2] + 2\)

      截屏2020-04-17下午4.30.46.png
      截屏2020-04-17下午4.30.46.png

    • 情况2:

      \(s[i - 1] == )\)

      这种情况下，如果前面有和\(s[i]\)组成有效括号对的字符，即形如\(( (....) )\)，这样的话，就要求\(s[i - 1]\)位置必然是有效的括号对，否则\(s[i]\)无法和前面对字符组成有效括号对。

      这时，我们只需要找到和\(s[i]\)配对对位置，并判断其是否是 \((\) 即可。和其配对对位置为：\(i - dp[i - 1] - 1\)。

      如果：\(s[i - dp[i - 1] - 1] == (\) :

      有效括号长度新增长度2，\(i\)位置对最长有效括号长度为 i-1位置的最长括号长度加上当前位置新增的2，那么有：

      \(dp[i] = dp[i - 1] + 2\)

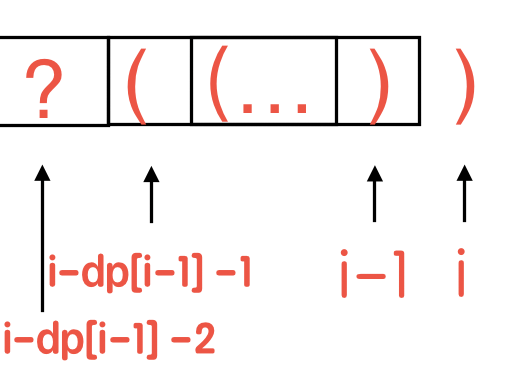
      值得注意的是，\(i - dp[i - 1] - 1\) 和 \(i\) 组成了有效括号对，这将是一段独立的有效括号序列，如果之前的子序列是形如 \((...)\) 这种序列，那么当前位置的最长有效括号长度还需要加上这一段。所以：

      \(dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2\)

注： 这个在分析时是很容易遗漏的，分析要更细致。我在第一次分析是就遗漏了，提交后，有用例 )()(()))不过，分析后发现是少了这一段。

截屏2020-04-17下午4.26.34.png
截屏2020-04-17下午4.26.34.png
子问题

根据上面的分析，我们得到了如下两个计算公式：

\(dp[i] = dp[i - 2] + 2\)

\(dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2\)

那么，求\(dp[i]\)就变成了求\(dp[i - 1]\)、 \(dp[i - 2]\)、\(dp[i - dp[i - 1] - 2]\)的子问题。

这样状态也明确了：

设\(dp\) 数组，其中第 \(i\) 个元素表示以下标为 \(i\) 的字符结尾的最长有效子字符串的长度。

转移方程

子问题明确后，转移方程直接由子问题得到：

1
2
3
4
5
6
7
8
if s[i] == '(' :
    dp[i] = 0
if s[i] == ')' :
    if s[i - 1] == '(' :
        dp[i] = dp[i - 2] + 2 #要保证i - 2 >= 0

    if s[i - 1] == ')' and s[i - dp[i - 1] - 1] == ')' :
        dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2 #要保证i - dp[i - 1] - 2 >= 0

初始条件和边界情况

初始条件： \(dp[i] = 0\)

边界情况：需要保证计算过程中：\(i - 2 >= 0\) 和 \(i - dp[i - 1] - 2 >= 0\)

计算顺序

无论第一个字符是什么，都有：\(dp[0] = 0\)

然后依次计算：\(dp[1], dp[2], ..., dp[n - 1]\)

结果是： \(max(dp[i])\)

复杂度计算

时间复杂度： 遍历了一遍字符串，所以时间复杂度是：\(O(N)\)

空间复杂度：需要和字符串长度相同的数组保存每个位置的最长有效括号长度，所以空间复杂度是：\(O(N)\)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int longestValidParentheses(string s) {
        int size = s.length();
        vector<int> dp(size, 0);

        int maxVal = 0;
        for(int i = 1; i < size; i++) {
            if (s[i] == ')') {
                if (s[i - 1] == '(') {
                    dp[i] = 2;
                    if (i - 2 >= 0) {
                        dp[i] = dp[i] + dp[i - 2];
                    }
                } else if (dp[i - 1] > 0) {
                    if ((i - dp[i - 1] - 1) >= 0 && s[i - dp[i - 1] - 1] == '(') {
                        dp[i] = dp[i - 1] + 2;
                        if ((i - dp[i - 1] - 2) >= 0) {
                            dp[i] = dp[i] + dp[i - dp[i - 1] - 2];
                        }
                    }
                }
            }
            maxVal = max(maxVal, dp[i]);
        }
        return maxVal;
    }
};

91.Decode Ways

结合题目，有方法的总数这个字眼，可以考虑尝试使用动态规划进行分析。这是一个计数型动态规划的题目。

疑惑确认

这个题目，对于“00”这种输入，是无法进行解码的，是否需要考虑输出应该是什么？题目中并没有完全说清楚。

输入"00"，测试结果是0，所以这种输入是支持的，代码中需要考虑。通过测试明确后开始分析。

首先，我们定义一个 \(dp\) 数组，其中第 \(i\) 个元素表示以下标为 \(i\) 的字符结尾的字符串的解码个数。

确定状态

最后一步

对于最优的策略，一定有最后一个元素 \(s[i]\)。

所以，我们先看第 \(i\) 个位置，这个位置的元素 \(s[i]\)可能有如下两种情况：

  • \(s[i] == '0'\) :

    这时，我们需要看\(s[i - 1]\)。

    如果 \(s[i - 1] == '0'\)，'0' 无法被解码，所以 \(dp[i] = 0\)。

    如果 \(s[i - 1] \ in\ ['1', '2']\)，这时\(s[i-1]s[i]\)只有一种解码方法，所以字符串可以变成

      s[0:i-2],  s[i-1]s[i]

    这样， \(dp[i] = dp[i - 2]\)

    如果 \(s[i - 1] >= '3'\)，这时 \(s[i-1]s[i]\) 无法被解码，所以 \(dp[i] = 0\)。

注：这儿的[0 : i-2]是全包含区间，下同。

  • \(s[i] > '0'\) :

    这时，也需要看\(s[i - 1]\)。

    如果 \(s[i - 1] == '0'\)，这时\(s[i-1]s[i]\)只有一种解码方法，所以字符串可以变成

      s[0:i-2],  s[i]

    这样， \(dp[i] = dp[i - 2]\)

    如果 \(s[i - 1] == '1' \ OR \ (s[i - 1] == '2' \ and \ s[i] <= '6')\)， 这时\(s[i-1]s[i]\)有两种解码方法，所以字符串可以变成

      s[0:i-2], s[i-1]s[i] 
  或
  s[0:i-1], s[i]

    这样， \(dp[i] = dp[i - 1] + dp[i - 2]\)

    如果 \((s[i - 1] == '2' \ and \ s[i] > '6') \ OR \ s[i - 1] >= '3'\)， 这时\(s[i-1]s[i]\)只有一种解码方法，所以字符串可以变成

      s[0:i-1],  s[i]

    这样， \(dp[i] = dp[i - 1]\)

子问题

根据上面的分析，我们得到了如下几个计算公式：

\(dp[i] = dp[i - 1]\)

\(dp[i] = dp[i - 2]\)

\(dp[i] = dp[i - 1] + dp[i - 2]\)

那么，求\(dp[i]\)就变成了求\(dp[i - 1]\)、 \(dp[i - 2]\)的子问题。

这样状态也明确了：

设\(dp\) 数组，其中第 \(i\) 个元素表示以下标为 \(i\) 的字符结尾的字符串的解码个数。

转移方程

子问题明确后，转移方程直接由子问题得到：

1
2
3
4
5
6
7
8
9
10
11
12
if s[i - 1] == '0' or s[i - 1] > '2':
    if s[i] == '0' :
        dp[i] = 0 # 出现连续两个0，后面无论是什么字符也无法进行解码了，所以可以直接return 0
    else:
        dp[i] = dp[i - 1]
else:
    if s[i] == '0' :
        dp[i] = dp[i - 2]
    else if s[i - 1] == '2' and s[i] > '6':
        dp[i] = dp[i - 1]
    else:
        dp[i] = dp[i - 1] + dp[i - 2]

其实，这个方程可以归纳为：

\(dp[i] = b0*dp[i - 1] + b1*dp[i - 2]\)

其中： \(b0/b1\)分别取值为0 或 1。取0或取1可以根据上面的条件得到。

初始条件和边界情况

初始条件： \(dp[i] = 0\)

边界情况：

首先，\(dp[0]\)根据第一个字符是否为‘0’得到。

需要注意\(dp[1]\)的计算，因为无法计算\(dp[1 - 2]\)。假如\(s = "10"\)，这时，\(dp[1] = dp[-1]\)，所以我们可以设\(dp[-1] = 1\)。

计算顺序

首先根据第一个字符计算\(dp[0]\)

然后依次计算：\(dp[1], dp[2], ..., dp[n - 1]\)

结果是： \(dp[n - 1]\)

复杂度计算

时间复杂度： 遍历了一遍字符串，所以时间复杂度是：\(O(N)\)

空间复杂度：需要和字符串长度相同的数组保存每个位置的最长有效括号长度，所以空间复杂度是：\(O(N)\)

我们计算\(dp[i]\)时，只需要用到\(dp[i - 1]和dp[i - 2]\)，所以可以只用两个变量把前面的两个值保存下来就行了，可以把空间复杂度降为\(O(1)\)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int numDecodings(string s) {
        int curways = 0;
        int preways = 0;
        if (s[0] > '0') {
            preways = 1;
            curways = 1;
        }

        for (int i = 1; i < s.length(); i++) {
            int tmp = curways;
            if (s[i - 1] == '0' || s[i - 1] > '2') {
                if (s[i] == '0') {
                    return 0;
                } else {
                    curways = curways;
                }
            } else {
                if (s[i] == '0') {
                    curways = preways;
                } else if (s[i - 1] == '2' && s[i] > '6') {
                    curways = curways;
                } else {
                    curways = curways + preways;
                }
            }
            preways = tmp;
        }
        return curways;
    }
};

139.Word Break

状态定义

设\(dp\)数组，其中第 \(i\)个元素表示以下标为 \(i\) 为结尾的字符串是否为拆分单词。

状态转移方程

\(dp[i] = {OR}_{0=<j<i}(dp[j] \ \ \&\& \ \ contains(wordDict, subStr(j,i-j)))\)

解释

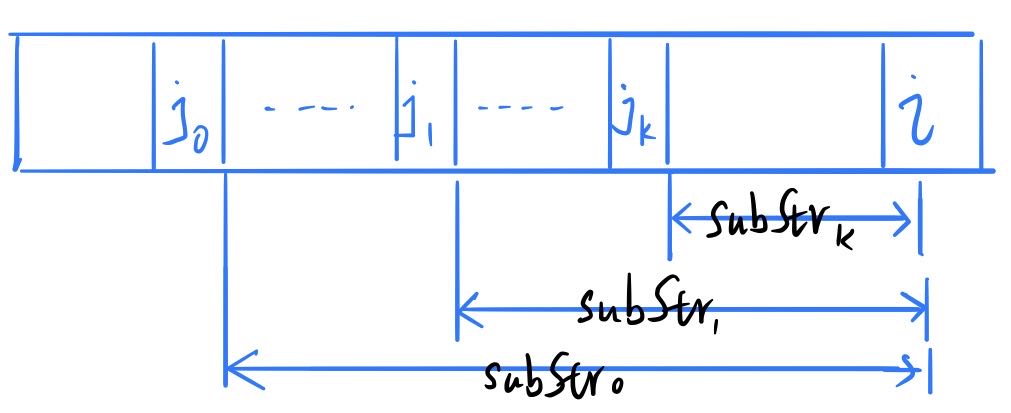
对于位置\(i\)，假设\(dp[j_k]=true\)，则只要\(subStr(s, j_{k+1}, i)\)这个子字符串在字典中，那么\(dp[i]=true\)，否则\(dp[i]=false\)。

所以，只需要找到所有的\(j_k\)，只要有一个满足上述条件即可。

WechatIMG1.jpeg
WechatIMG1.jpeg

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        int len = s.length();
        vector<bool> dp(len + 1, false);
        dp[0] = true;

        for (int i = 1; i <= len; i++) {
            for (int j = i - 1; j >= 0; j—) {
                if (dp[j] && find(wordDict.begin(), wordDict.end(), s.substr(j, i - j)) != wordDict.end()) {
                    dp[i] = true;
                    break;
                }
            }
        }

        return dp[len];
    }
};

1025. Divisor Game

归纳法可以得出 “偶数赢，奇数输”，这样的话这个题目就没啥意义了。

这个题目可以思考用动态规划的方法解决，就是前面提到的博弈型动态规划。

随着游戏的进行，黑板上的数越来越小，这样可以想到子问题，把大数慢慢降为小的数。

状态转移方程

设\(dp[i]\)表示数字i时，爱丽丝是否能赢。

爱丽丝先手，她可以选择的数是i的所有满足 \(0 < x < i\) 的因子。下一手为鲍勃，如果鲍勃能赢则爱丽丝必输，否则爱丽丝能赢。x的值可能有多个，只要爱丽丝选择能赢的那一个即可，也就是说，只要有一个选择能赢，爱丽丝就可以赢。

所以 \(dp[i] = OR(!dp[i - x]), x满足 i \% x == 0 \ and \ \ 0 < x < i\)

这样就得到了状态转移方程。

初始值： \(dp[0] = false, dp[1] = false\) , dp[0]其实用不到，因为 x < i。

结果是：dp[N].

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool divisorGame(int N) {
        vector<bool> dp(N + 1, false);

        for (int i = 2; i <= N; i++) {
            for (int f = 1; f <= i / 2 && i % f == 0; f++) {
                if (!dp[i - f]) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[N];
    }
};

221. Maximal Square

72. Edit Distance

总结

拿到动态规划类型的题目后，不要慌，根据题目中是否有：计数、最大/最小/最长、是否存在等字眼，先判断是否可以使用动态规划解决，如果可以，然后根据上面的步骤，一步一步进行分析，尤其是最后一步这一步分析，是能否转化为子问题的关键。转化为子问题后，就能轻易得到转移方程，后面的操作就简单了。

有些题目，动态规划不一定是最高效的解法，但是根据这个套路进行分析，一定是最快的解法。先写出来之后再考虑是否可以优化，或者其他更优的解法。